13/02/2007 1 – Matemática

Introdução a conjuntos

A= {elementos}

A= ∅ ou {} (vazio)

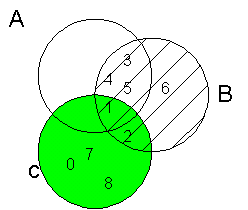
Diagrama de Veen

União:

União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A ou B.

Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A e B, simultaneamente.

Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B.

 

 

Seja:

A = {1,2,3} e

B = {0,1,4,5}

Pede-se:

a) A U B = {0,1,2,3,4,5}

b) A ∩ B = {1}

c) A – B = {2,3}

d) B -A = {0,4,5}

 

 

 

********************************************************************************

Seja:

A = {0,1,2,3,4,5} e B = {0,1,2} representar por diagrama:

 

Conjunto A contém conjunto B.

Conjunto B está contido em A.

B ⊂ A.

a) A U B = {0,1,2,3,4,5}

b) A ∩ B = {0,1,2}

c) A – B = {3,4,5}

d) B – A = ∅

Sejam os conjuntos:

A = {1,3,4,5}

B = {1,2,3,4,5,6}

C = {0,1,2,7,8}

 

 

 

a) (A – B) ∩ (B -C) =

∅ ∩ {3,4,5,6} = ∅

ATENÇÃO: Intercecção com vazio, é sempre vazio!

Seja A = {0,1,2,3,4} e B = {2,3,4,5} , pede-se:

a) (A ∩ B) U A = {0,1,2,3,4} = (A)

b) (A U B ) ∩ B = {2,3,4,5} = (B)